அட ஆச்சரியம்! சாய்வு பாதை, அரை விட்டம் பாதை, L-வடிவ பாதை. இந்த மூன்றிலும் மூன்று பந்தை ஒரே நேரத்தில் உருட்டினால்..

அட ஆச்சரியம்! சாய்வு பாதை, அரை விட்டம் பாதை, L-வடிவ பாதை. இந்த மூன்றிலும் மூன்று பந்தை ஒரே நேரத்தில் உருட்டினால்.. 

சாய்வு பாதை வழியாக வரும் பந்து தான் முதலில் சேரும் என நான் நினைத்தேன், ஆனால் அது தவறு, அந்த பந்து கடைசியாக தான் சேர்ந்தது. அரை விட்டம் பாதை வழியாக வரும் பந்து தான் 2 வது வந்து சேரும் என எண்ணுகையில் அதுவும் தவறு. அந்த பந்து தான் முதன் முதலில் சேருகிறது. 3 -வது பந்து சேரும் பாதை என நான் நினைத்தது, L வடிவ பாதை -அதுவும் தவறு தான்.இதன் வழியே வரும் பந்து இரண்டாவதாக வந்து சேருகிறது. நாம பொதுவாக நினைத்து ஒன்று, இயற்பியல் விதிப்படி நடப்பது ஒன்று. உலகிலேயே தலைசிறந்த ஒரு விஞ்ஞானியும் கணிதவியல் பேராசிரியராக இருந்த ஸ்டீவன் ஹாக்கிங். இவர் உருவாக்கிய இயற்பியல் கணித கோட்பாட்டால் அண்ட சராசரத்தையும் அதனுள் மறைந்திருக்கும் பெருவெடிப்பு கொள்கையையும் உலகத்துக்கு அறிமுகபடுத்தினார். இத்தனைக்கும் இவர் நரம்பியல் நோயால் பாதிக்கப்பட்டு கை கால் செயலிழந்து பேச்சு ஆற்றலும் இல்லாமல் வீல் சேரிலேயே அமர்ந்து கொண்டே உலகை வியக்கும் உன்னத கோட்பாட்டை உருவாக்கினார். இப்போது தான் புரிகிறது இவரது கல்வி. வானங்கள் பூமியின் சூத்திரங்களை இயற்பியல் கணிதத்தின் விதிப்படியே அழகாக தெரியவைத்தார். 

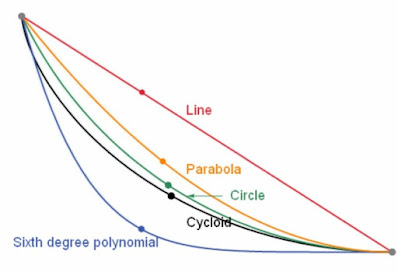
உண்மையில் கல்வி கற்றவர் உயர்ந்தவர், கல்வியின் அருமை காலம் கடந்து புரிகிறது. சரி, மூன்று பந்துகள் உருண்ட காட்சியை கண்டு, இதன் விளக்கத்தை அறிய இணையத்தில் சென்றேன். "பிராச்சிஸ்டோக்ரோன் & சைக்ளோயிட்டின்" என்ற விதியின் கோட்பாடு என தகவல் கிடைத்தது. இந்த வார்த்தையை இப்போ தான் அறிகிறேன், இதை எழுத்து கூட்டி நிதானமாக வாசித்தாலும் வாயில் நுழையமாட்டேங்குது. விதியின் கோட்பாட்டு குறியீடுகளை நீங்களும் அறிய விரும்பினால் இந்த லிங்கை கிளிக் செய்து உள்ளே உள்ள பதிவில் போங்கள், மூன்று பந்துகள் உருண்டது போல நம் தலையும் சேர்த்து நான்காவது பந்தாக உருளும். ஒன்னுமே புரியாது. ஆனால் படித்தவர்களுக்கு இது சப்ப மேட்டர் என கடந்து செல்வார்கள்.

 

பிராச்சிஸ்டோக்ரோன் சிக்கலை ஜோஹான் பெர்னோலி கணித உலகிற்கு சவாலாக அறிவித்தார்.(இது அவரே கண்டறிந்த சிக்கல்தான்) நியூட்டன், லெப்னிட்சு முதலிய பெருங்கணித தலைகளுக்குச் சவாலாக அறிவித்தார். நியூட்டனுக்கும் பிறநாட்டு அறிஞர்களுக்கும் ஆகவே ஆகாது. இருப்பினும், பெயர் வெளியிடாமல் இந்த சிக்கலுக்கான தீர்வை வெளியிட்டார். பிராச்சிஸ்டோக்ரோன் என்றால் கிரேக்கமொழியில் குறைவான நேரம் என்று பொருள் கொள்ளலாம்.

 

பிராச்சிஸ்டோக்ரோன் கேள்வி:

A என்பதை ஒருப்புள்ளியாகவும் , அதன் கீழே சற்றே தள்ளி B என்பதை ஒருப்புள்ளியாகவும் கருதினால், இவ்விரு புள்ளிகளையும் இணைக்கும் எந்த வடிவம் குறைந்த நேரத்தை எடுத்துக்கொள்வதாக அமையும்? ஈர்ப்புவிசையினைக் கவனத்தில் கொள்ளவும். 

இதனைத் தீர்ப்பதற்கு, பியரி டி ஃபெர்மாட் எனும் பிரெஞ்சு கணிதவியலறிஞரின் ஒளி பற்றிய ஒரு கூற்று உதவக்கூடும். எந்த இரண்டு புள்ளிகளையும் கடக்க, ஒளியானது குறைந்த நேரத்தைக் கொள்ளும் பாதையைத் தேர்ந்தெடுக்கும். இப்போது, ஒளியானது வெவ்வேறு ஊடகங்களில் பயணிக்கும் போது,அது பல அடுக்குகளை(layers) கடந்து செல்லும். ஒவ்வொரு அடுக்கிலும் அதன் வேகம் மாறுபடும். அனைத்து அடுக்குகளிலும் அது பயணித்த பாதையை வரையும்போது, ஒரு வளைவு வடிவம் கிடைக்கிறது.

மேற்புறத்திலிருந்து தான் இருக்கும் அடுக்கு வரையுள்ள தொலைவு. (y) தன் பாதைக்கு வரையப்பட்ட தொடுகோட்டிற்கும்(tangent to the curve) , அதற்கு வரையப்பட்ட செங்குத்துக்கோட்டுக்கும் (normal) இடையேயான கோணம். (sine of the angle). இந்த இரு பண்புகளுக்கான விகிதம் எந்தவொரு அடுக்கிற்கும்,ஒரு மாறிலியாக இருக்கும். இந்த பார்வை, இந்த கேள்விக்குப் பொருத்திப் பார்க்கும்பொழுது, விடை கிடைக்கிறது.

பிராச்சிஸ்டோக்ரோன் (enbrachistochrone) சிக்கல்

 https://ta.quora.com/piraccistokron-cikkalai-evvaru-kanita-ritiyaka-tirkka-mutiyum

 சைக்ளோயிட்டின் வளைவு 

https://syzpc.ru/ta/baths-saunas-equipment/naiti-dlinu-dugi-pervoi-arki-cikloidy-parametricheskoe-uravnenie/

 சைக்ளோயிட்டின் அளவுருக்கள்

https://syzpc.ru/ta/metal-metal-products-fasteners/specialnye-ploskie-krivye-parametricheskoe-uravnenie-cikloidy-i-uravnenie/

 

ஏம்பா, ஆட்டோக்காரா சம்மந்தமில்லாத இடத்தில் தலைய நுழைச்சி மூளை புகைஞ்சது தானே மிச்சம், கடைசிக்கு வரைக்கும் மூன்று பந்து உருண்ட விசயம் புரியல உனக்கு, என எனக்குள் பேசிகொண்டு அந்த பதிவிலிருந்து வெளியேறினேன். "கற்பதும், கற்பிப்பதும் இறை நம்பிக்கையே" எனும் மகுடத்தை சூட்டுகிறது இஸ்லாம். இது தான் கல்வியின் சிறப்பு, கல்வி கற்கும் வயசையும் வாய்ப்பையும் இழந்து விடாதீர்கள்.

நன்றி: தக்கலை ஆட்டோ கபீர்.