Today (February 23, 1855) is the anniversary of the birth of Carl Friedrich Gauss, the greatest mathematician of all time in the world of mathematics.

Johann Carl Friedrich Gauss was
born on April 30, 1777, to poor, working-class parents in Brunswick, Duchy of
Brunswick-Wolfenbettel. His mother was illiterate. He never recorded his date
of birth. He only remembered that he was born on a Wednesday. Eight days before
the Ascension Feast (which is 39 days after Easter), Gauss later solved this
riddle about his date of birth in the context of finding the date of Easter.
Obtained instructions for calculating the date in past and future years. Father
Keppard was an ordinary poor worker. Before becoming a second wife to his
mother Dorothy Keppard, she worked as a housekeeper. At the age of three, Cass
discovered something wrong with his father's payroll.

As soon as he entered the
classroom one day at the age of seven, the boy Gauss finished an account given
to him by the teacher to keep all the students from speaking. It is a
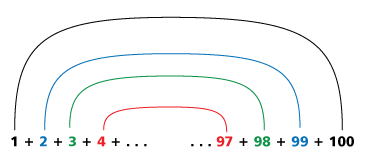
calculation of the sum of integers from 1 to 100. It immediately appeared to Gauss
that there were 50 pairs of numbers from 1 to 100. I.e., (1, 100), (2, 99), (3,
98), etc. The sum of each is 101, so the sum of 50 pairs is 5050. The teacher
is overwhelmed by the student. He approached his parents asking for permission
to teach the boy all the intricacies of mathematics beyond school hours. They
were illiterate at the birth of the mathematical world. Otherwise, they would have
done the same thing that the musician Wolfgang Mozart's father had done to
bring him to town, thinking of making his son's predictable talent a visual
object.

From the age of eleven to four
years, Gauss received a good education in archaeology. But more important than
that was the education he received in mathematics, which he read directly and
spontaneously. I had the opportunity to learn the whole of Newton's Principia
'and Bernoulli's' excellent texts such as' Ars Conjugandi'. By the age of 15,
the late Lord Ferdinand of Brunswick, who had seen the high standard of his
education, had helped him by giving him an incentive to study in college.
Within three years of studying in college, he had given two guesses for the
number pi (n). The student, who plays with prediction problems daily, has calculated the values of pi (n) to be n = 3,000,000 to test his
own formulas.

Gauss studied for three years at
the University of Gottingen. But from his reference books, published many years
after his time, it seems that he was more attracted to archaeology teachers than
to mathematics teachers in Gottingen. However, after learning about the Ferma
particles and the solution given by Euler that the sixth Ferma number F5 is not
a prime number, he came to the conclusion that other Ferma numbers could not be
participles. After this, he decided that his future was in mathematics and not
in archaeology. Determined that he had no teachers to guide him in Gottingen, he
returned to his hometown of Brunswick and began writing dissertations for his
doctorate. The object he took for it was the basic theorem of algebra. That is,
the theorem that there will be n solutions at the complex site for each
in-sequence polynomial equation with complex complexes.

In 1799 he was awarded a
doctorate by the University of Hemstead for this study. That theory still bears
his name today. What is even more remarkable is that he gave three more
installations in his lifetime for this experiment. The last installation gave
in his 70s. Gauss was one of the first mathematicians to equate complex points
to the points of a site and to free the notion of 'problem', which is now
unnecessarily fabricated in the name of complex numbers, with each point (a, b)
representing a complex number (a + ib). The desire to filter out what came to
his mind from the age of 17 into a book became Disquisitiones arithmeticae in
1798, and in 1801 at the age of 24, he became a great treasure in the world of
mathematics and arithmetic. In fact, it cannot be said that there was a theory
of numbers before that. Because all that is known about numbers from Greek
times to the present day are many separate theorems. No one found Fermat,
Euler, Lagrange, and Legendre in a position to combine them into one theory.

Gaussin's equivalent, modulo n's
concept helped to combine many of their ideas. In the fourth chapter of Gazin's
book, Quadratic Residues are taken. Legend had already discovered a delicious
rule of thumb. It is a matter of matching two components, (p, q), that is, two
theories as to whether they are duplicates or non-duplicates. Studies have
shown that since the time of the Greeks, the only way to draw a polygon is to
use a baton and an axe. They knew the outline of the order polygon on pages 3,
4, 5, 6, 8, 10, 15. But many have failed to find the definition of the order
polygon on pages 7, 9, 11, 13…, etc. Gauss just found that an order polygon
with pages of odd numbers n must have a numerator or a multiple of n if they
are to be drawn with two integers.

It was not until he discovered
this at the age of 18 that he began writing a diary for his mathematical
discoveries. His diary was placed before the world 43 years after his death.
According to Gauss' discovery, the Gregor could only draw pages 3, 5, 15, 17,
257, 65537, or pages with a multiplication of them, with the order polygonal
curvature. Co-augmentation has been a major headache for the mathematical world
since Euclid's time. Over the centuries many have tried to dismantle the need
to keep it as a premise without getting any installation for it. Finally, in
the 19th century, Lobachevsky and Boley separately found a solution to this
problem in a way that would bring about a fundamental change in mathematics.
But Gauss had gone the same way before them and had written in his diaries with
the consent of his mind to the same changes. Thus all three are still said to
be the fathers of Euclidean geometry.
The Gaussians did not regard him
only as a mathematician. This is because his gravitational pull has long been
in the geographical dimensions of pioneering mathematics. Who was involved in
them at a young age? Fifteen years after being fascinated by the theory of
autonomic arithmetic, he devoted himself to the disciplines of autonomous
mathematics, such as geography. In 1817 he was given the responsibility of
surveying the area of Hanover. Considering the uselessness of the gauges of
the time, he invented a new device called the heliotrope. In addition, driven
by his predictability, he made several subtle changes in the measurements
made with these quantities and improved their quality. More important than all
of this was measuring the angular dimensions of large triangles and testing
whether there was evidence in the light world for his Euclidean geometry. He
did the large triangular size that had been done until then.
The broken peak at 1142 m, 20 km. The
farthest peak is Inselburg (915 m), 12 km southwest of Gottingen. Peak
Hoharhagen (508 m) in the distance measured all three angles of the triangle.
The sides of this triangle are 70, 110 km. However, the sum of the three angles
was 180 '0' 15 ". His non-Euclidean geometric prediction expected a
further difference from the 180 vortexes. ) To respond to him with the findings
of the findings, 'I knew all this beforehand,' and the Hungarian father and son
misunderstood him.

On January 1, 1801, Piaggi
discovered the first asteroid and tried to look at it a short distance through
a telescope in the western sky and again in the lower sky, but missed the
accuracy of the astronomical predictions. Gauss accurately predicted these
predictions, pointing to a place 14 lunar phases away from that particular
location, where the asteroid (named Sirius) was found. The 24-year-old young
scientist became world-famous. Laplace was one of the most important French
mathematicians of the time. When asked who Germany's best mathematician was, he
said 'Pfaff'. 'You may have forgotten the case. The answer he gave was that Gauss
is the best mathematician in the world.

The best mathematician of all
time in the world of mathematics. He made significant contributions in all four
fields: mathematics, physics, astronomy, and geography. In mathematics, he laid
the foundation of numerology, geometry, and differential geometry in many ways.
He was a man of immense power in predictions and made achievements in
astronomy, geography, and number theory. The great mathematician Carl Friedrich
Gauss passed away on February 23, 1855, in Gottingen, Germany, at the age of 77.
Source By: Wikipedia
Information: Dr. P. Ramesh, Assistant Professor of Physics, Nehru Memorial College, Puthanampatti, Trichy.
Get information like this
https://t.me/joinchat/jpqj3jQLN51kYTk9
Join Telegram Group.
https://chat.whatsapp.com/FisIzCe4Br2CRgxAiicUnf
Join WhatsApp Group
Thanks.
Also, Read
🛑👍 CSIR-NET Physics Materials and Problems
🛑📕 21 GB and Hundreds of Physics E-Books Collection.
🛑🛥️ How does an Electric Motor work? (DC Motor).
🛑🤹♂️ Science Academies' Summer Research Fellowship Programme for Students and Teachers 2022.
🛑🔌 How does a Transformer work - Working Principle electrical engineering.
🛑🎙️ Transistors Explained - How transistors work.
🛑🔥⚡ How Thermocouples Work - basic working principle.
🛑🔌 Voltage Explained - What is Voltage? Basic electricity potential difference
🛑🔌 What is CURRENT– electric current explained, electricity basics.

.jpg)

No comments:
Post a Comment