கணிதத்தில் நாம் பயன்படுத்தும் அநேகக் குறியீடுகளை அறிமுகம் செய்த லியோனார்டு ஆய்லர் நினைவு தினம் இன்று (செப்டம்பர் 18, 1783).

கணிதத்தில் நாம் பயன்படுத்தும் அநேகக் குறியீடுகளை அறிமுகம் செய்த லியோனார்டு ஆய்லர் நினைவு தினம் இன்று (செப்டம்பர் 18, 1783).

லியோனார்டு ஆய்லர் (Leonhard Euler) ஏப்ரல் 15, 1707ல் சுவிட்சர்லாந்தில் உள்ள பாசெல் என்னுமிடத்தில் பவுல் ஆய்லர் என்பவருக்கும், மார்கரீட் புரூக்கர் என்பவருக்கும் மகனாகப் பிறந்தார். தந்தை பவுல் ஆய்லர் சீர்திருத்தத் திருச்சபையைச் சேர்ந்த ஒரு மதகுரு. தாயாரும் ஒரு குருவானவரின் மகளே. ஆய்லர்க்கு இரண்டு தங்கைகள் இருந்தனர். ஆய்லர் பிறந்ததுமே ஆய்லர் குடும்பத்தினர் பாசெல்லிலிருந்து ரீஹென் என்னும் நகருக்கு இடம் பெயர்ந்தனர். பவுல் ஆய்லர், அக்காலத்தில் ஐரோப்பாவில் பெயர் பெற்ற கணிதவியலாளரான ஜொஹான் பர்னோலி என்பவரின் குடும்பத்துக்கு நண்பராக இருந்தார். இது இளம் ஆய்லரின் கணித ஆர்வத்துக்குப் பெரும் பங்களிப்புச் செய்தது. இளம் வயதிலேயே அதீத ஆற்றல் கொண்ட ஆய்லர், தாம் படித்த புத்தகங்களில் தோன்றும் குறிப்புகளை ஒரு வார்த்தைகூடப் பிறழாமல் பல ஆண்டுகளுக்குப் பின்பும் அப்படியே ஒப்பிக்கும் நினைவாற்றல் பெற்று விளங்கினார். இளம் வயதிலேயே தனது கணித ஆற்றலை வெளிப்படுத்தத் தொடங்கினார்.

 

ஆய்லர் படித்த பள்ளியில் கணிதம் பாடமாகவே இல்லை. அதனால் கணிதத்தில் ஆர்வமுடைய இவருடைய தந்தை இவரை ஜான் பெர்னோவிலி என்ற ஒரு புகழ் பெற்ற கணிதப் பேராசிரியரிடம் தனி மாணவனாகப் பாடம் கற்றுக் கொள்ள அனுப்பித்தார். ஆனால் பெர்னோவிலி இவரை சனிக்கிழமைகளில் மாத்திரம் வரச்சொல்லி உன் சந்தேகங்களைக் கேட்டுக்கொள் என்று சொல்லிவிட்டார். அதுவே ஆய்லருக்கு ஒரு வரப் பிரசாதமாகியது. ஏனென்றால் கணிதம் கற்றுக் கொள்ள இதைவிட வேறு நல்ல வழி கிடையாது என்று ஆய்லரே பிற்காலத்தில் சொல்லியிருக்கிறர். அவருடைய உழைப்பையும் கத்திமுனை புத்தியையும் பார்த்த இன்னும் இரு பெர்னோவிலிகள்தான் (டேனியல் பெர்னோவிலி, நிக்கொலாஸ் பெர்னோவிலி இருவரும்) இவன் பெரிய கணித மேதையாவான் என்று கண்டுகொண்டு, மதப் படிப்பில் இவரை ஈடுபடுத்த முயன்ற தந்தையின் மனதை மாற்றினார்கள்.

இன்று கணிதத்தில் இவர் பெயர் கொண்ட கருத்துக்கள், சூத்திரங்கள் மற்றும் தேற்றங்கள் நூற்றுக்கும் மேல் உள்ளன. அந்த அளவுக்கு அனைத்துக் கணித உட்பிரிவுகளிலும் தனது ஆதிக்கத்தைச் செலுத்தி மாபெரும் மேதையாக ஆய்லர் கணித உலகில் சஞ்சரிக்கிறார். கணிதத்தில் இன்று நாம் பயன்படுத்தும் அநேகக் குறியீடுகளை இவரே அறிமுகம் செய்தார். உதாரணமாக, சார்புகளைக் குறிக்கும் ƒ(x) குறியீடு, கூடுதல் மதிப்புக்கான Σ குறியீடு, முக்கோணவியல் சார்புகளான sin x, cos x போன்ற பெயர்கள், மடக்கை அடிமானமான e என்ற குறியீடு, கலப்பு எண்ணின் i என்ற கற்பனை அலகு போன்றவை குறிப்பிடத் தக்கவையாகும். கணித உலகில் இரு எண்களைத் தன் பெயரில் கொண்ட ஒரே கணித மேதை ஆய்லர். மடக்கை சார்புகளின் அடிமானமான e என்ற எண்ணைக் கண்டறிந்து அதன் தோராய மதிப்பை 2.718 என வழங்கினார். இன்று இதை ‘ஆய்லர் எண்’ என அழைக்கிறோம். அதேபோல் காமா (ϒ) எனும் மாறிலியையும் இன்று ‘ஆய்லர் மாறிலி’ என அழைக்கிறோம். இதன் மதிப்பு 0.57721 என தோராயமாக அமைகிறது. காமா எனும் ஆய்லர் மாறிலி விகிதமுறு எண்ணா, அல்லது விகிதமுறா எண்ணா என இன்றுவரை கூற இயலவில்லை.

                                         

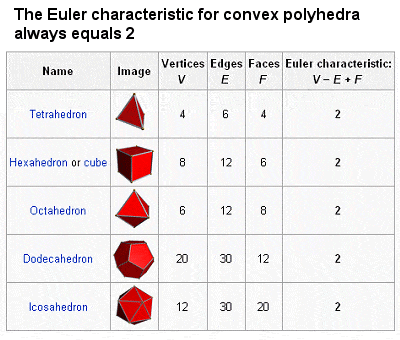
இன்று கணிதத்தில் மிகச் சிறப்பான சூத்திரமாகக் கருதப்படும் eiπ+1= 0 என்ற சமன்பாடை இவர் வழங்கிய eiθ= cos θ + i sin θ சூத்திரத்திலிருந்து θ = π எனப் பிரதியிட்டுப் பெறலாம். கோநிஸ்பெர்க் பாலக் கணக்கு எனும் கணிதப் புதிருக்கு இவர் வழங்கிய தீர்வு மூலம் Graph Theory எனும் கணித உட்பிரிவு உருவானது. அதேபோல், ν-e + ƒ=2 என்ற பன்முகி சூத்திரம் Topology எனும் கணித உட்பிரிவு தோன்ற வழிவகுத்தது. மேலும், பொருட்களின் தொடர்புகளைப் படங்கள் மூலம் வெளிப்படுத்தும் பண்பை வரைபடங்கள் மூலம் ஆய்லர் வெளிபடுத்தினார். இன்று இவ்வரைபடங்களை நாம் ஆய்லர் வரைபடங்கள் என அழைக்கிறோம். இவையே இன்று நாம் கணங்களில் தற்சமயம் பயன்படுத்தும் வெண் வரைபடங்களின் மாதிரியாகத் திகழ்கின்றன. 

1736ல் ஆய்லர் மக்களின் கவனத்தை ஈர்த்த ஒரு பிரச்சினையை விளையாட்டுப்போல் எளிதில் விடுவித்தார். அந்த பிரச்சினையும் அதன் நிறுவலில் இருந்த தத்துவமும் மூன்று நூற்றாண்டுகளுக்குப் பிறகு இடவியல், கோலக்கோட்பாடு என்ற இரண்டு தற்காலக் கணிதப் பிரிவுகளுக்கு அடிக்கோலிட்டது. ஒரு ஆறு, அதில் இரண்டு பெரிய தீவுகள். ஆற்றின் குறுக்கே ஏழு பாலங்கள். ஏழு பாலங்களையும் ஒரு நடையில் கடக்கவேண்டும். போன பாலத்திலேயே இரண்டாம் முறை போகக்கூடாது. இது முடியுமா? இதுதான் பிரச்சினை. கோனிக்ஸ்பர்க் மக்களுக்கு இது உண்மைப் பிரச்சினை. ஏனென்றால் அவர்கள் ஊரில் தான் இத்தீவுகளும் பாலங்களும். மக்கள் நடந்து நடந்து சோதனை செய்தே அயர்ந்தனர். ஆய்லர் இதை நுண்பியப்படுத்தி கணித முறைத் தர்க்கத்தினால் விடுவித்தார். அவருடைய தீர்ப்பு ஏழு பாலங்களையும் ஒரு நடையில் கடக்கமுடியாது. 

ஆய்லர் கணித மரபுப்படி பிரச்சினையிலிருந்த சம்பந்தமில்லாத விஷயங்களை ஒதுக்கிவிட்டு, அதன் அடித்தளத்திலிருந்த உயிர் நாடிப்பிரச்சினையை வெளிக்கொணர்வதற்காக, பாலங்கள் பிரச்சினையை கோலம் மூலமாக எளிதாக்கினார். நிலப்பரப்புகள் ஒவ்வொன்றையும் ஒரு புள்ளியாகவும், பாலங்களை அவைகளை இணைக்கும் கோடுகளாகவும் (அவை நேர் கோடாக இருக்கவேண்டிய தேவையில்லை) செய்ததில் ஒரு கோலமாகியது. 4 கோணப்புள்ளிகளும் 7 இணைக்கும் கோடுகளும் உள்ள இந்தக் கோலத்தில், ஒருபுள்ளியிலிருந்து 5 கோடுகளும் மற்ற 3 புள்ளிகளில் ஒவ்வொன்றிலிருந்தும் 3 கோடுகளும் செல்கின்றன. இந்த சூழ்நிலைக்கு ஆய்லர் ஒரு கணிதத் தேற்றத்தையே நிறுவினார். அதாவது, எல்லா கோடுகளையும் கடக்கக்கூடிய ஒரு நடை இருக்க வேண்டுமென்றால், ஒன்று, எந்தப் புள்ளியிலிருந்தும் ஒற்றைப்படை எண்ணிக்கையுள்ள் கோடுகள் செல்லக்கூடாது, அல்லது, இரண்டே புள்ளிகளிலிருந்து ஒற்றைப்படை எண்ணிக்கையுள்ள கோடுகள் செல்லவேண்டும்.

 

இந்த கோனிக்ச்பெர்க் பாலப்பிரச்சினையில், 4 புள்ளிகளிலிருந்தும் ஒற்றைப்படை எண்ணிக்கையுள்ள கோடுகள் செல்வதால், நடை சாத்தியமில்லை. இதற்கும் இடவியலுக்கும் என்ன சம்பந்தமென்றால், இந்தப்பிரச்சினையில் புள்ளிகளிலிருந்து செல்லும் கோடுகள் எத்தனை என்ற ஒரே கேள்விதான் பிரச்சினையின் வேர். இந்த வேர் பிரச்சினையில் வேறு வடிவியல் விவகாரம் இல்லை. புள்ளிகளிலிருந்து எத்தனை கோடுகள் செல்கின்றது என்பது கோலத்தை எவ்வளவு கோணலாக்கினாலும் அதாவது, கோடுகளை நீட்டி, மடக்கி, வளைத்தாலும் மாறாமலிருக்கும் ஒரு எண். இந்த மாதிரி கருத்துகளைத்தான் இயற்கணித இடவியல் ஆய்வு செய்கிறது. கணிதத்தில் மிக அதிகமான படைப்புகளை வழங்கியதோடு மட்டுமல்லாமல் பல அழகு பொருந்திய சூத்திரங்களை ஏற்படுத்தி, கணிதத்துக்குப் பொலிவூட்டியவர் ஆய்லர். மேலும், பல நவீன கணித உட்பிரிவுகளுக்கு இவரது சிந்தனைகளே அடித்தளமாக அமைந்தன. இவரது படைப்புகள் கிட்டத்தட்ட 30 ஆயிரம் பக்கங்களுக்கு மேல் நீள்பவை. இவர் கண்டறிந்த செய்திகளின் பட்டியலை நூற்றாண்டுகளுக்கு மேல் சேகரித்து அப்படைப்புகளின் சிறுகுறிப்புகளை நூறு தொகுதிகளுக்கு மேல் வழங்கியுள்ளனர். இதிலிருந்து இவரது படைப்பாக்கத்தின் பிரம்மாண்டத்தை நாம் உணரலாம்.

முப்பது வயதில் தனது வலது கண்ணை இழந்த ஆய்லர், தனது அறுபதாவது வயதில் மற்றொரு கண்ணையும் இழந்தார். இருப்பினும் அதன் பிறகு அவர் வாழ்ந்த 16 ஆண்டுகளில் வாரத்துக்கு ஓர் கண்டுபிடிப்பை நிகழ்த்தி அனைவரையும் ஆச்சரியத்தில் ஆழ்த்தினார். தினமும் காலை முதல் மாலை வரை தனது கண்டுபிடிப்புகளைக் குறிப்பதற்கென ஓர் நபரை நியமனம் செய்து அவர் மூலம் பதிவு செய்ததாக அறியப்படுகிறது. முதல் அறுபது ஆண்டுகளில் உருவாக்கிய கணிதப் படைப்புகளுக்கு இணையான கணிதப் படைப்புகளை பிற்காலத்திலும் அவர் உருவாக்கினார் என்பது அவரது அற்புத நினைவாற்றல், விடாமுயற்சி, உழைப்பு போன்றவற்றின் வெளிப்பாடே. கணித உலகத்தில் இவையெல்லாம் புது முன்மாதிரிகளாக அமைந்தன.

 

கணிதம் மட்டுமல்லாது இயற்பியல், வானியல், திரவ இயக்கவியல், ஒளியியல், இசைக் கோட்பாடு போன்ற பல்வேறு துறைகளிலும் கருத்துகளை வழங்கியுள்ளார். இவரது பெருமையை, பிற்காலத்தில் தோன்றிய பிரெஞ்சு கணித அறிஞரான லாப்லாஸ் இவ்வாறு குறிப்பிடுகிறார்: “ஆய்லரைப் படியுங்கள், ஆய்லரைப் படியுங்கள், அவர்தான் நம் அனைவருக்கும் ஆசான்”. கணிதவியல் மற்றும் அறிவியல் அறிஞர் லியோனார்டு ஆய்லர் செப்டம்பர் 18, 1783ல் தனது 76வது அகவையில் இரஸ்சியா, சென் பீட்டர்ஸ்பேர்க் நகரில் இவ்வுலகை விட்டு பிரிந்தார்.

Source By: Wikipedia

தகவல்: இரமேஷ், இயற்பியல் உதவி பேராசிரியர், நேரு நினைவு கல்லூரி, புத்தனாம்பட்டி, திருச்சி.

இது போன்ற தகவல் பெற
https://t.me/joinchat/Ex0_TNk_10WnjXOc
இந்த Telegram  குழுவில் இணையவும்.
https://chat.whatsapp.com/JLgK0szSQzoGrB39M90W94
இந்த WhatsApp  குழுவில் இணையவும்.

நன்றி.
தகவல்: இரமேஷ், இயற்பியல் உதவி பேராசிரியர், நேரு நினைவு கல்லூரி, புத்தனாம்பட்டி, திருச்சி.

                                                       மேலும் படிக்க 

🛑🤔 நாம் பிறந்ததில் இருந்து நம் உடலில் வளராத உறுப்பு எது?

🛑✍️ TNPSC-ஆன்லைனில் தமிழக அரசு இலவச பயிற்சி.

🛑✍️ தேசிய அளவில் 35,000 ரூபாய் வரை கல்வி உதவித்தொகை பெற ஓர் வாய்ப்பு -National Scholarship Exam (NSE – 2021).

🛑🚀 இஸ்ரோ(ISRO) வழங்கும் இலவச ஆன்லைன் கோர்ஸ்- ISRO MOOC Course on the “Remote Sensing for Agriculture (two days short course).

🛑✍️நீங்கள் நினைத்தவை எல்லாம் நடக்கிற வாழ்க்கை ரகசியம்- காணொளி.

மிகவும் பயனுள்ள வீடியோ அனைவருக்கும் பகிர்க.